Persamaan F . Δt = Δp yang telah kita turunkan menyatakan bahwa momentum suatu sistem dapat berubah jika ada gaya dari luar yang bekerja pada sistem itu. Tanpa adanya gaya luar ini momentum sistem tidak berubah (Δp = 0) atau momentum sistem kekal. Sebagai gambaran kita tinjau sebuah senapan yang menembakkan peluru.
Sistem kita anggap terdiri atas peluru dan senapan. Pada sistem ini tidak ada gaya luar yang bekerja, sehingga kita harapkan momentum sistem tidak berubah. Setelah peluru ditembakkan ternyata senapan tertolak ke arah belakang.
Apakah benar momentum sistem tidak berubah?
Bukankah momentum peluru mengalami perubahan setelah penembakan?
Memang benar momentum peluru mengalami perubahan yaitu dari nol (sebelum penembakan), menjadi tidak nol (sesudah penembakan)! Akan tetapi kita harus ingat bahwa senapan juga mengalami perubahan momentum. Momentum senapan setelah penembakan ini sama dengan
momentum peluru, tetapi arahnya berlawanan. Akibatnya momentum sistem (momentum senapan + momentum peluru) sama dengan nol, yaitu sama dengan momentum mula-mula. Dengan kata lain momentum kekal.

Perhatikan Gambar 5.3 di atas. Di sini dua buah bola yang masingmasing bermassa m1 dan m2 bergerak dengan kecepatan v1 dan v2 (gambar (a)). Kemudian kedua benda bertumbukan
( gambar (b)) dan setelah bertumbukan kecepatan masing-masing benda menjadi v1’ dan v2’.
Karena tidak ada gaya luar yang bekerja pada sistem tersebut, maka momentum sistem kekal, artinya momentum sebelum dan sesudah tumbukan sama.
p sebelum tumbukan = p sesudah tumbukan

Persamaan tersebut dinamakan Hukum Kekekalan Momentum yang menyatakan:
"Jika tidak ada gaya luar, maka momentum sistem sebelum dan sesudah tumbukan kekal".
ROKET
Setelah roket dijalankan maka pada roket akan didapat percepatan. Percepatan yang diperoleh roket ini mirip dengan percepatan yang diterima oleh senapan setelah menembakkan pelurunya.
Percepatan roket diperoleh dari tolakan gas yang disemburkan roket itu. Tiap molekul gas dapat dianggap sebagai suatu peluru kecil yang ditembakkan roket. Dalam sistem ini momentum total roket dan momentum gas senantiasa sama selama tidak ada gaya luar (diabaikan). Jika gaya gravitasi yang bertindak sebagai gaya luar tidak diabaikan, ia akan mengurangi momentum roket.
Misalkan mula-mula kecepatan roket v dan massa roket m, anggap roket menyemburkan gas sejumlah Δm, sehingga kecepatan bertambah menjadi v + Δv. Kecepatan semburan gas anggap sebesar vg (Catatan: kecepatan roket dan kecepatan gas diukur relatif terhadap suatu acuan, misalnya bumi).
Catatan:
Δm . Δv diabaikan karena kecil dibandingkan dengan suku yang lain (Δm saja sudah kecil apalagi jika dikalikan dengan Δv tentu lebih kecil lagi bukan?) Percepatan roket dapat dihitung sebagai berikut:
sering disebut laju semburan gas (banyaknya semburan gas tiap detik). v + vg adalah sama dengan kecepatan roket relatif terhadap gas dan sering ditulis vr sehingga persamaan percepatan rata-rata roket adalah:
Jika medan gravitasi tidak diabaikan, medan gravitasi akan memberikan percepatan ke bawah sehingga percepatan roket (atau sering disebut dengan percepatan lontar) menjadi:




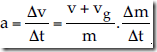
















0 comments:
Post a Comment